Torsion points on elliptic curves

The main object of arithmetic geometry is to find all the solutions of Diophantine equations.

Examples:

Find all the rational numbers X and Y such that

X2 + Y2 = 1

Find all the rational numbers X and Y such that

X2 + Y2 = 3

Find all the rational numbers X and Y such that

Y2+2 = X3

The main idea is the following: consider the solutions (X,Y) in the real plane, and use geometric technics to determine the rational solutions.

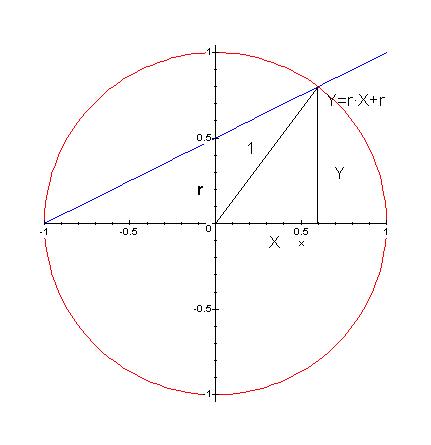
Let's consider the first example:

X2 + Y2 = 1

The zero locus of this equation in the real plane is the radius 1 circle.

Now, consider a point in the circle with rational coordinates. For example:

(1,0) or (0,1) or (-1,0) or (0,-1)

I will use (-1,0) but any other will work.

Now, any straight line passing through (-1,0) cuts the circle on another point (except the vertical line).

What are the points that have rational coefficients? Exactly the ones such that the slope of the line is rational.

Algebraically:

A (non vertical line) is

Y = r ·X + s

for some r (slope) and s.

The line contains (-1,0) if 0 = r ·(-1)+s, that is if s = r.

So the lines we are considering are the ones with equation

Y = r ·X + r

Now, the intersection with the circle of radius 1 is the simultaneous solution of this equation with

X2 + Y2 = 1

Replace Y by r ·X + r in this last equation. We get

X2 + (rX+r)2 = 1

hence

(1+r2)X2+ 2r2X + r2-1 = 0

Now, the solutions of this equation are

X =  -2r2 ±2 2(r2+1) =  ì ï ï í ï ï î -1    1-r2 1+r2

The solution X = -1 is the one we already know. The other solution is

(X,Y) =  æ ç è 1-r2 1+r2 , 2r 1+r2 ö ÷ ø

So, we can see that if r is a rational number, X and Y are rational numbers (and viceversa).

We just found a (well known) parametrization of the circle.

So we have a formula for all the rational solutions of X²+Y² = 1.
 
 

Non arithmetic application:

We know that the points of the circle can be parametrized by using trigonometric functions. They are the points:

(cos(q), sin(q))

Now, it is not hard to see that r is the tangent of  q / 2.

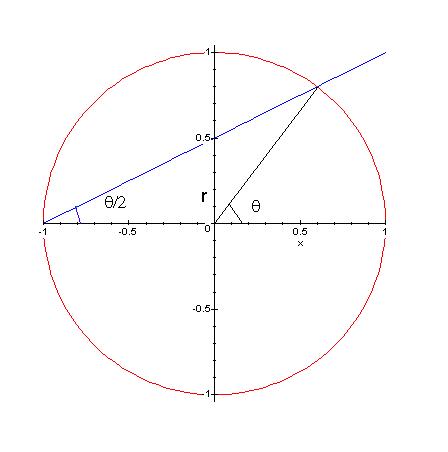
So, we get the equations: If

r = tan æ ç è q 2 ö ÷ ø

then

cos(q) =  1-r2 1+r2   and  sin(q) =  2r 1+r2 .

These equations can be used to transform any trigonometric integral to a rational integral.
 
 
 

Why this method works? Two reason's:

• We have a solution.
• Any straight line cuts the circle in 0, 1 or 2 points.

Fact: If we have a quadratic equation with rational coefficients and we know one rational solution, then there are an infinite number of solutions and they can be parametrized in terms of one parameter.
 
 

More examples:

The equation X²+Y² = 2. We have an obvious rational point (1,1) (or (-1,1), (1,-1), (-1,-1)). Consider this last point: (-1,-1). Lines containing this point: Y = rX+(r-1). Intersection with the circle:

(X,Y) =  æ ç è - r2-2r-1 1+r2 ,  r2+2r-1 1+r2 ö ÷ ø

The equation

3X-XY+6-2Y = 1

(is an hyperbola).

We have a rational point (-1,2).

Applying the same method we get that the solutions (other that (-1,2)) are:

(X,Y) =  æ ç è - 2r-1 r , 3-r  ö ÷ ø .

 

Now, consider the equation in the beginning:

X2 + Y2 = 3

At first sight it has no solutions.

How we know? Transform it to a problem about integer solutions (X = A/C and Y = B/C):

A2 + B2 = 3C2

Has integer solutions (A,B,C) different from (0,0,0), and such that A, B and C are coprime?

First: 3 cannot divide A or B. Since if it does, it divides A, B and C, hence they are not coprime.

Second: Do modulo 3. We get

A2 + B2 º 0 (mod 3)

which has no solutions (different from (0,0)).

General answer (Legendre):

To know if a quadratic equation has no rational solutions, first see if it has real solutions.

If it does, transform it to a quadratic equation (in three variables) and look for integral solutions.

Now, there is an integer m (computable in terms of the coefficients of the equation) such that the integral equation has solutions if and only if it has solutions modulo m.

Let's go to the next case: what happens with the cubic equations?

Claude Gaspar Bachet de Méziriac (1581-1638).  

He is most famous for his Latin translation of Diophantus's Greek text Arithmetica (1621) in which Fermat wrote his famous Last Theorem marginal note.

In one of his books, he says the following:

Let c be a rational number. Suppose that (x,y) is a rational solution of the equation

Y2 = X3+c.

Then

(  x4-8cx 4y2  ,  -x6-20cx3+8c2 8y3  )

is also a rational solution.

How did he found this formula? No idea.

But we have a geometric interpretation of it.

The idea starts as before: Consider the zero locus of

Y2 = X3+c.

If (x,y) is a rational solution of the equation, consider a straight line through (x,y). Now, this line cuts the curve in 2 more points (or less); and even, this 2 points have not necessarily rational coordinates!

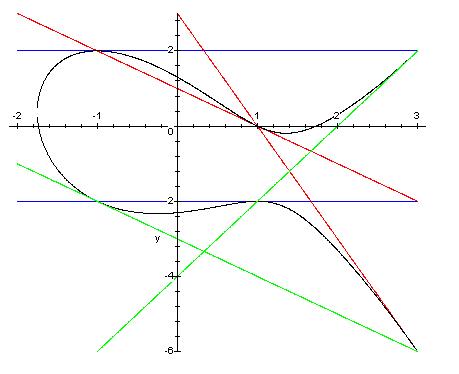
Example: If c = -2, we have the solution (3,5). Now, the lines that go through (3,5) are Y = rX+(5-3r). If you substitute Y by rX+(5-3r) and expand, and then you divide by X-3 (it always divide), one gets that the X coordinates of the other points of intersection are the solutions of

-X2+r2X-3X-3r2+10r-9 = 0

For example, for r = 1 we get

-X2-2X-2 = 0

with no real solutions! And for r = 3, we get

-X2+6X-6 = 0

with solutions 3 ±Ö3.

So, what can we do? Consider the line that cut "two times" the curve in (x,y): the tangent line.

From the relation

Y2 = X3+c

we get by implicit derivation that the slope of the tangent line at (x,y) is 3x²/2y.

In our case c = -2 and (x,y) = (3,5) we get the line with slope r = 27/10. Applying in the formula we obtain

-X2+  429 100 X- 387 100

with solution X = 3 and X = 129/100.

You can see is the same number that in Bachet's formula.

In general, Bachet's formula gives use the coordinates of the intersection between the tangent line at (x,y) and the curve.

Applying this formula one gets:
 
 

( 129 100 , 383 1000 )

( 2340922881 58675600 , 113259286337279 449455096000 )

( 30037088724630450803382035538503505921 3010683982898763071786842993779918400 ,

- 164455721751979625643914376686667695661898155872010593281 5223934923525719974563641453744978655831227509874752000 )

and so on...

You can see that the numbers "increase" a lot (they don't increase in size, but in "height", that is the size of the integers giving the reduced form of the rational numbers appearing). This is a general fact, but this is another history...

In general, consider an equation of the form

Y2 = X3+aX2+bX+c

They are called elliptic curves.

If the equation is non-singular, one can use the following procedure:

Suppose we know a rational solution (x,y).
 

• Compute the tangent line of the curve at this point.

• Compute the intersection with the curve.

• The point you obtain is also a rational solution.

Formula: If (x,y) is a rational solution, then (x¢,y¢) is another rational solution, where

x¢ =  x4-2bx2-8cx+b2-4ac 4y2 .

So, it seems that we have found a procedure to compute infinitely many solutions if we know one. But this is not true!

For example, if y = 0, x¢ is not defined (or better, it is equal to infinite).

Another example: if x¢ = x, and y¢ = y, we get no new point.

Problem: what else could happen?

Beppo Levi (1875-1961)

He conjectured in 1908 that there is only a finite number of possibilities, and gave the exact list.

This conjecture was made after him by T. Nagell (1952), A. Ogg (1971).

Finally, B. Mazur proved this conjecture in 1977 in a celebrated paper.

Barry Mazur    

Theorem (Mazur)

Let (x,y) be a rational point in an elliptic curve. Compute x¢, x¢¢, x¢¢¢ and x¢¢¢¢. If you can do it, and all of them are different, then the formula before gives you infinitely many different points.

In modern language:

If (x,y) is a rational torsion point in an elliptic curve of order N, then N £ 12 and N ¹ 11.

Examples:
 
 

Y2+Y = X3-X2

and the point

(x,y) = (1,0)

One has that x¢¢ = x (and y¢¢ = -y).

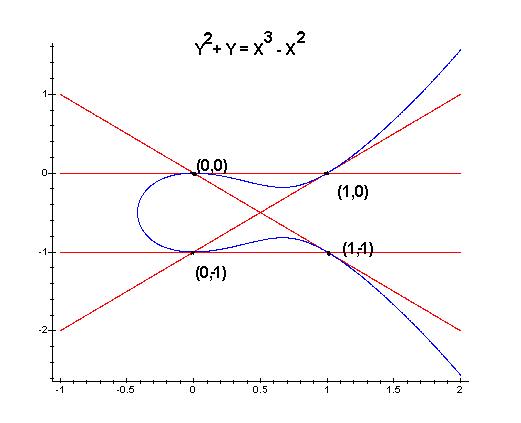
(to get an equation like before, substitute Y by Y-1/2)
 
 

Y2+XY+Y = X3-X2-3X+3

and the point

(x,y) = (1,0)

One has that x¢¢¢ = x (and y¢¢¢ = -y).

(to get an equation like before, substitute Y by Y-1/2(X+1))

Further developments:

L. Merel in 1996 proved, using the work of a lot of people like Kammieny, Manin, Faltings, Kolyvagin, Logachev, the following result.

Theorem:
For any integer d ³ 1, there is a constant B_d such that for any field K of degree d over Q and any elliptic curve over K with a torsion point of order N, one has that N £ B_d  .

P. Parent found an specific constant, which is exponential in d.

Conjecture:  There is a constant which is polynomial on d.

Theorem (Hindry-Silvermann): If E has good reduction everywhere, then N £ 1 977 408 d log(d)

What happens if we have curves of higher degree? (In more technical terms, of higher genus).

A similar conjecture can be done:
 

Conjecture: For any g ³ 1, there exists a constant C_g such that, for any abelian variety of dimension g (e.g. the jacobian of a curve of genus g) defined over Q, and any rational torsion point of exact order N, then N £ C_g.

Nothing is known about this conjecture.
 

Theorem There is an specific constant C(g,p) such that any abelian variety of dimension g defined over Q such that it's reduction at p does not contain G_m, and any rational torsion point of exact order N, then N £ C_g.

Conjecture If g = 2, N = 31 cannot appear.