Hyperbolic
perpendicular line
To
plot the perpendicular for a point we will distinguish two cases: the
point belongs to the line or the point is exterior to the line.
Point in the line
In
Absolute Geometry it is known that can be plotted one and only one
perpendicular line to a line that goes through a given point. To
construct the hyperbolic perpendicular we will use a similar way to
the one that we used for the perpendicular bisector.
To plot the hyperbolic perpendicular we need a hyperbolic line and a
point
that belongs to this straight line. To assure that
the point belongs to the line, first we mark two
points, to construct the straight line and then we mark a point in the
constructed line.
- Construct
the hyperbolic line that goes through the two
given points.
- Mark the
point, P, of the line where
we want to plot the perpendicular.
- Plot the
tangent line to the plotted hyperbolic line in the step
(1) that passes
through the point P. To
construct this line we can plot the normal straight line,
from the radius and to consider its perpendicular.
- Plot the
circumference that passes through P and
has center in the intersection point between the tangent
line and the boundary line.
- Consider
the two intersection points between this circumference and the
boundary line.
- Plot the
arc with origin in one of the point of former intersection, passing
through P and ending in the
other intersection point.
This is the perpendicular line that we wanted to construct.
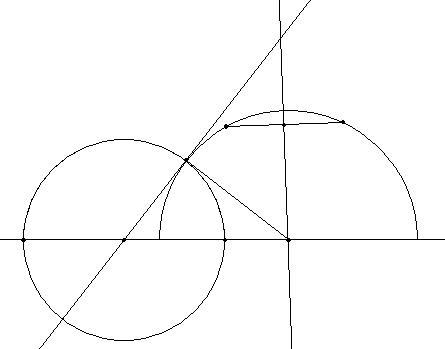
To prove that this
hyperbolic line we have constructed is the perpendicular line, it is
enough seeing that it forms right
angles with the initial line. As in the
case of the bisector angle, we have that this is true because we can
find an inversion with center in the boundary line that assures us that
the angles are right angles.
The inversion which it is necessary to consider is the same
circumference which we search to prove that the constructed line is the
perpendicular line.
This circumference has the center, O, in the boundary line. To prove
it, we can consider any line going through the center of the inversion
and intersect with the given hyperbolic line in two points, C and D. The power from the
point O
in the
hyperbolic line allows us to affirm that: OP·OP=OC·OD and to be OP the radius of
the circumference of inversion we obtain that points C and D are inverse. So, the
angle formed by the circumference of
inversion and the segment PC transforms
into the angle formed by the same circumference and the segment PD.
As these two angles are adjacent and equal they are, by definition,
right angles. From here we can affirm that the plotted hyperbolic
line is the perpendicular.
It is necessary to
remark that on using this tool, it will not ask
us for the third point, but it will put one point by default. To obtain
the perpendicular from the point that we want, we have only to move the
point that the program has given us.
Exterior point
To construct the
perpendicular in the case that the point is exterior to the line we
will use the hyperbolic bisector and the parallel lines.
We know that given a hyperbolic line and an exterior point exists one
and only one perpendicular line to the given line that goes through the
point. This affirmation is true since it can be proved in the Absolute
Geometry. To be able to use this tool, we have to give three points.
The two first points will determine the line and the third point we
will suppose that it is the exterior point. In this construction we
will
suppose that the hyperbolic line is a semicircumference with
center in the boundary line.
To construct the perpendicular line for an exterior point we will
follow
these steps:
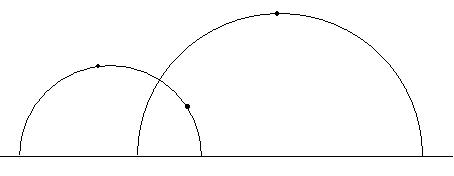
- Construct
the hyperbolic line that goes through the two
first
points.
- Construct
the two parallel lines to the hyperbolic
line just constructed and that go through the third point.
- Follow
the steps that allow us to construct the angle
bisector but only until the
step (14). We have constructed the circumference that contains the
bisector.
- Plot
the arc of circumference that will determine the perpendicular line.
Consider the arc with origin in one of the two intersection points
between the former circumference and the boundary
line, going through P and
finishing in the other
intersection point.
In this way we
can determine the perpendicular from an exterior point. All steps are
well defined, if we suppose that the two given points do not belong to
a perpendicular line to the boundary line, since
they use constructions which we already know that, in this situation,
we can always make. The plotted line is perpendicular
because we have constructed it from the parallel lines and we
know that given an exterior point, if we plot the perpendicular for
this
point and the parallel lines we have that the angles that each
one of the parallel lines forms with the perpendicular are equal. So,
if we have the two parallel lines and another line
that divides the angle that they form, this line will be the
perpendicular line since it will fulfill the same properties as the
perpendicular line and we know that it is unique.
List of tools
Hyperbolic
geometry